Numerical Renormalization Group and the Kondo Problem
Lecturer: Andrew K. Mitchell
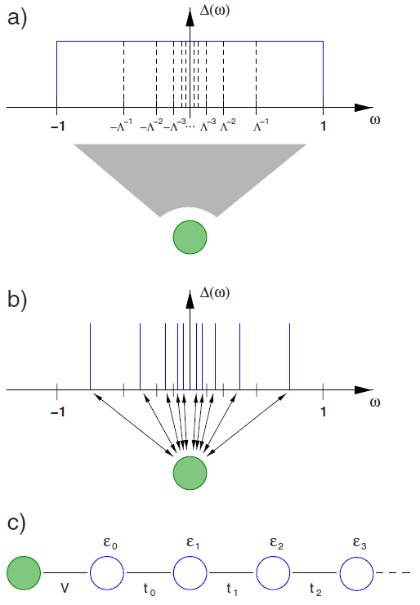
'Quantum Impurity Problems' are classic paradigms for strong electron correlations in condensed matter physics. They underpin the theoretical description of magnetic impurities in metals, nanodevices such as quantum dots, and appear as effective models within the dynamical mean field theory of correlated materials. Non-perturbative quantum many-body methods must be employed to solve such problems. In this course, we provide the conceptual framework of the Numerical Renormalization Group, discuss technical/practical details of the calculation, and present relevant applications.
Lecture slides in pdf format:
Part 1: Quantum Impurity Problems and theoretical background.
Part 2: Kondo effect and the Renormalization Group.
Part 3: Wilson Chain and the RG in NRG.
Part 4: Results and Applications.
References
(opens in a new window)K. G. Wilson, Rev. Mod. Phys. 47, 773 (1975)
(opens in a new window)A. C. Hewson, "The Kondo problem to heavy Fermions" (CUP, 1997)
(opens in a new window)H. R. Krishnamurthy, J. W. Wilkins, and K. G. Wilson, Phys. Rev. B 21, 1003 (1980)
(opens in a new window)R. Bulla, T. Costi, and T. Pruschke, Rev. Mod. Phys. 80, 395 (2008)
Exercises:
1) Schrieffer-Wolff transformation
2) Perturbative scaling for the Kondo problem
3) Tutorial NRG code: try it yourself!